Forward-Euler

The forward-Euler method truncates the Taylor series after two terms:

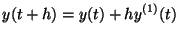$$y(t+h) = y(t) + hy^{(1)}(t)$$ (1.2)

Assuming that the value at point 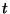$t$ is correct, the forward-Euler method computes the value at point 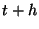$t+h$ with a local error that scales with 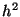$h^2$ (see the first term of the error series). The forward-Euler method always gives overshoots on the original curve.

Figure 1.1: Graphical illustration of the forward-Euler method for an exponential like curve. Starting at point 1, the tangent of the curve is taken and linearly extrapolated to obtain point 2. There again the same procedure is used to obtain point 3. Note that point 2 lies on curve 2 and point three lies on curve 3, both of which are offset against the original curve.